【al sherbin】用概率交易期權——策略選擇

注：本文截取於al sherbin2015年3月出版的最新著作“how to price and trade options——identify, analyze and execute the best trade probabilities”，cii獨家編譯，轉載自cii芝加哥投資學院。

本書中，作者將期權規則分為“界定風險”和“非界定風險”兩大類。每一個大的類別中，各種規則按照其適用的不同隱含波動率環境加以分類。作者按照三個子類別進行介紹：低波動率、高波動率、其他（或一般）波動率。

到目前為止，我們已經選擇了一個標的，它的流動性很高、並且基於某種關於波動率的假設能為我們帶來一定優勢。在此我想要澄清一下，你並不需要和我的想法完全相同才能獲得成功。我身邊有很多朋友在交易上十分成功，但所使用的方法和參考的指標都完全不同。

事實上，幾乎很少有兩個成功的交易員想法完全一致。這也是期權交易的魅力所在。只要你了解期權定價及交易背后的概率論和數學方法，你就擁有充足的創新空間。很多時候在芝加哥期權交易所的交易大廳里，我和其他的專業做市商互相交易，但卻能夠雙方獲利。他們可能是在平倉已有頭寸、轉移風險，而我可能是基於自己的計算愿意以當前價格的承擔他們的風險，並認為該價格具有獲利空間。

話雖然這么說，期權的隱含波動率卻是需要我們探索的最大“變量”。所以不難想到，隱含波動率的相對水平不僅僅要用於選擇標的，也要用於選擇規則。一些規則利用的是隱含波動率上漲，一些規則利用的是隱含波動率下降，而另外一些是“波動率中性”的。我們對於股票或隱含波動率未來走勢的假設將決定我們使用哪些規則來獲得最大優勢。

在我們具體介紹各種規則之前，需要注意的一點是你們交易所使用的賬戶類型可能會影響你能夠使用的規則類型。比如說，如果你用ira賬戶，或任何其他的現金賬戶進行交易，那么你將無法做空股票或做空裸看漲期權。然而，你可以賣出看漲價差或交易備兌看漲期權。你也許可以賣出裸看跌期權，因為它比單純購買股票風險略小。

但總的來說，賬戶類型會約束你的規則，並限制你希望達到的資金回報率。一些經紀商還會進一步對你進行約束，如果他們真這么做了，我建議你認真考慮換一家經紀商。我前面所述的限制是法律唯一規定的，其他任何限制都是經紀商附加的，而且采取這些限制條款往往是由於經紀商的懶惰或對產品的風險特征缺少認知。

這些可能的限制包括禁止空頭跨式期權、空頭寬跨式期權、空頭裸看漲期權（包括作為比率價差的一部分）。他們要求你的上端敞口必須是“界定”風險，但是下端可以具有“非界定”風險，因為股票價格理論上最多跌到零，但可以無限上漲。

盡管對於期權規則的討論有很多種不同的分類方法，但根據前文所述的原因，我傾向於將期權規則分為“界定風險”和“非界定風險”兩大類。這種分類方法對於新手交易員和賬戶規模較小的交易員來說尤為重要。界定風險交易通常對保證金的需求要比非界定風險交易小得多，因此更適合小賬戶。另外，界定風險交易的最大損失通常相對較小，或可以設置為較小額度，因此對新手交易員來說，在其經驗不足的學習階段中能夠限制損失。

在每一個大的類別中，我會將各種規則按照其適用的不同隱含波動率環境加以分類。我會按照三個子類別進行介紹：低波動率、高波動率、其他（或一般）波動率。雖然我不打算深入介紹希臘值，但我會簡單回顧一下vega和theta，在我們的討論中對這些希臘值的了解是至關重要的。如果你還不熟悉希臘值的概念，我建議你花幾分鐘的時間上網搜尋一下這個主題，這些概念很簡單，你應該可以從上千個網站上免費獲得足夠的資訊。正是對希臘值的靈活運用，能夠使你在交易中獲得優勢，我們將在本書中不斷印證這一點。現在，讓我們開始逐個討論一些常用的規則。

同樣的，如果你對這些我即將討論的規則不了解，請自行上網學習。我假設你已經熟悉每種規則，我將不會介紹這些規則是什么，而是僅僅討論這些規則該如何應用。

界定風險交易

據上文所述，界定風險交易非常適合初學者和小賬戶。但我必須實話實說，雖然交易界定風險和非界定風險規則的原則相同，我的絕大部分盈利來自非界定風險規則。對界定風險規則的使用，就好比我在自行車上裝了輔助訓練車輪。雖然這輛車也能帶我去任何想去的地方，但是速度要慢得多。它們幫助我學習騎車，使我免受重傷。我可以用它們來熟悉一個新的標的、一種新的規則、一次高風險情景或一個新的交易平臺，而不需要承受太多資金風險。然而一旦準備好了卸下這些輔助車輪，你的表現會好得多。我相信每一位交易員在具備了一定的財務實力和交易技巧后，都應該更傾向於非界定風險的規則——但在此之前，我們應該從界定風險的規則著手進行學習。

貸方價差

不是所有的貸方價差都彼此相同。這句話實際上適用於所有價差規則。假設你交易的股票價格是＄30，這支股票的各期權執行價格之間的差距可能是＄1，也可能是＄0.5。在其中一個貸方價差中，你可能以＄0.35的價格賣出了＄28/＄29看跌價差；而在另一個貸方價差中，你可能以＄1.25的價格賣出了＄31/＄36看漲價差。雖然二者都具有界定的風險，它們的風險特征、購買力減少量和希臘值都具有極大區別。希臘值在期權的規則交易中起重要作用，而這三個方面都應該在交易之前加以考慮。我們就用上面這兩筆交易來舉例，看一下它們的風險特征、購買力減少量和希臘值之間的差別。

首先我們來看28/29看跌價差，我們以＄0.35的價格賣出。就像所有的空頭價差或空頭裸期權一樣，我們能從這筆交易中獲得的最大收益就是所收取的權利金。因此在這個例子中，我們最多可以賺＄0.35。我們會損失多少？在最差情境下，我們的最大損失是價差執行價格的寬度減去收取的權利金。在我們的例子中，最大損失是（29-28）-0.35=＄0.65。如果要承擔＄0.65的風險來獲取＄0.35，為什么還要做這筆交易呢？一如既往，概率論將帶給我們這個問題的答案。如果我們在該筆交易中獲利的概率大於65%，而損失的概率小於35%，那我們在該筆交易中就獲得的正的預期收益。這是否意味著每次出現這種交易時我們都應該去賣呢？我們如何知曉盈利預期是多少？

第一個問題的答案取決於該交易的資金回報率，以及與其他可行交易的資金回報率相比較。總得來說，我們希望能夠最大化每一美元投資的回報率。因此，如果我們認為盈利的概率站在我們這邊，那么這個＄0.35的貸方價差應該是我們所選擇的交易。由於該價差的最大損失為＄65，因此這也是你的經紀商預計你應該事先存入的保證金的金額。因此，如果我們在交易中獲得了最大收益＄35，那么我們的資金回報率就是＄35除以＄65，約等於54%。

如果我們的價差還有30天到期，這將給我們帶來令人驚艷的646%的年化收益率！為什么我們不全用這種價差來交易呢？答案在之前所講過的章節中。期權交易確定的優勢取決於對期權隱含波動率的有效利用。當隱含波動率處於百分比的高位，而且標的變動緩慢並小於期權的隱含波動率時，我們就能從空頭期權的交易中獲得優勢。

如果我們的波動率假設是正確的，那么該筆交易的效果主要是由vega來衡量的。一個較窄的價差（一到兩個執行價格寬度）通常來說vega相對較小，特別是與單獨賣出一個期權相比。事實上，對於我們上面所舉例的這種單位執行價格的價差而言，該價差的vega僅為單獨做空一個期權的vega的四分之一。排除了波動率的邊際優勢，我們的界定風險交易幾乎趨近於一個“零和遊戲”，當然也不完全如此，因為還有另外一個優勢來源。另外的優勢來自於隱含波動率要高於歷史（實現）波動率。雖然在短時間內，這種優勢未必每次都能體現出來，但在大多數的交易中我們總能獲得這一優勢。

雖然大多數學者和投資顧問都將“資金回報率”當成神聖的標準，而說到底還是風險和回報之間的關係起決定性作用。如果我對每天所承擔的風險水平滿意，那么我的底線盈利能力才是我唯一真正需要考慮的指標。我寧愿以稍大一點的風險（感到舒服並可管理的）來賺取＄100,000，而不是以更小的風險賺取＄50,000。但如果賺取＄100,000所需要承擔的風險與其回報不相稱，那我也很愿意接受＄50,000，如果后者相對來說風險回報能夠達到平衡。

考慮到這一點，讓我們來關注一下前面所提到的第二個價差組合。在第二個組合中，我們賣出了＄31/＄36看漲價差，獲得＄1.25的權利金。這意味著我們以＄3.75的風險來賺取＄1.25。我們試圖用更大的風險來獲得較低的資金回報率，然而總體回報金額更高一些。如果獲得最大收益的話，我們的資金回報率是33%，假設30天到期，年化資金回報率為396%。

但盡管我們為每一個組合支付了＄375的保證金，該筆交易真正的風險是多少呢？你可能會說極端事件確實會發生，你真正的風險就是＄375。然而，這些極端事件是十分罕見的。實際上，經紀商和清算所都不以極端事件來衡量交易員的風險，我認為交易員自己也不應該這樣來衡量。正如在“退出交易”一章將要討論的，在每筆交易開倉之前，我就應該想好我的退出點在哪里。如果交易正合我意，那么在哪里退出；如果交易與我的預料相反，那么應該在哪里退出。正是我所選擇的退出點決定了該筆交易的認知風險。雖然我不能用該數字來計算資金回報率，但我可以將其用在自己的風險回報分析中。

讓我們舉個例子來說明。我們假設在賣出31/36看漲價差之前，我們計劃當價格觸到＄0.25或＄3.00時就將該價差購回，無論哪一個價格先被觸發。這意味著在這筆交易中，我們要么會賺取＄1.00的收益，或損失＄1.75。盡管有可能發生隔夜缺口，使得我沒辦法以＄3.00的價格買回該價差，但應該也不至於會超過＄3.00太多。因此，我認為這筆交易的風險是＄1.75（我所選擇的止損水平），而非＄3.75的保證金水平。再回到之前關於vega的討論中來，這個價差組合的寬度是5個單位執行價格，它的vega要遠遠高於第一個組合的vega。所以，利用我們的波動率假設，這個價差組合能夠獲得更多的邊際優勢。而且，同樣的，如果我們我們所選擇的退出點不是該價差的最大損失點，這些較寬的價差作為長期規則來說具有更高的獲利潛力。另外，如果你是用現金賬戶進行交易（比如ira），這些較寬的看漲價差是模擬裸空頭期權的最佳規則。對小賬戶來說也是如此。

貸方價差還有一個特征，它是方向性規則。即使股票變動很多，它也必須向你的反方向變動才能使你遭受損失。

另外，我們對交易的選擇還基於它如何影響整個投資組合。我們將在投資組合管理一章中更詳細的闡述這一點。

借方價差

在本書中我幾乎不太討論不收集theta的規則，借方價差就是其中之一。之所以如此，是因為我的期權交易是利用概率來獲得邊際優勢，借方價差通常不具備這種優勢。然而它具備大多數多頭期權交易共有的優勢。當以某種形式組合時，借方價差可以形成約為50/50的賺錢概率。盡管沒有獲得概率的青睞，該借方價差可以在交易中以中性的預期價值實現某些其他功能。借方價差是純粹的方向交易，但與股票交易不同，它具有有限的風險和收益。它的保證金要求也比較有限，可以允許你在方向賭注上安心的增加杠桿。它也可以增加投資組合的delta，用來降低總方向敞口，雖然它的效果有限，因為它是一個具有界定風險的規則。

如果你購買一個虛值的借方價差，你每晚都要為這個組合付錢，該組合賺錢的概率小於50%。雖然這要比我前面推薦的借方價差價格便宜，但如果長期購買，我認為你一定會賠錢。從來沒人告訴過你買期權會賠錢嗎？那讓我來告訴你吧！

那么，我們要如何構建一個50/50的借方價差組合呢？做法是，購買一單位執行價格實值期權，然后賣出一單位執行價格虛值期權，組合的整體價格約等於價差寬度的一半。我們假設xyz交易價格為＄30。如果你買入一個執行價格29的看漲期權，賣出一個執行價格31的看漲期權，組合價格為＄1，你的賺錢概率就大約為50%。很明顯，如果股票漲了，你就賺錢，如果股票跌了，你就賠錢。該價差幾乎不受波動率變化的影響。但通常由於“基差”的影響，這種價差很少以完美對稱的形式出現。股利和利率可能會影響其對稱性。另外，波動率偏度也會造成輕微影響。

如果使用一單位實值和一單位虛值的期權來構建價差的效果更好，那為什么不買一個借方價差，使其兩邊都是實值的呢？這樣不是會進一步增加盈利概率嗎？是的，這樣會提升概率。但是，一個多頭的實值借方價差與一個空頭的虛值貸方價差是等價的。貸方價差收取權利金，而不像借方價差要提前支付一筆現金；虛值貸方價差更容易成交，且被分配行權的風險遠遠小於實值借方價差。我們來分別解釋一下這幾個問題，這些細節不僅僅對理解借方價差很重要，如果你不了解這些，說明你在期權實戰交易中缺少一些重要的知識。

回想我們之前討論過的合成期權，讓我們來舉個例子。如果xyz的交易價格為＄63，我們以＄3.50的價格購買＄55/＄60看漲價差，這與我們以＄1.50賣出＄55/60看跌價差是等價的。兩筆交易都是以＄3.50的風險博取＄1.50，回報點也完全相同。

與其事先支付＄350來購買組合，何不先賣出看跌組合來收取＄150呢？另外，我猜看漲價差在市場上更難以操作，因為這些期權的價格要高得多。隨著價格升高，買賣報價的價差也會變寬。在討論價差的公允價值時這些細節比較不明顯，除非你對合成期權的概念了如指掌！

最後，當你處理實值看漲期權時，如果股票分發股利，價差中的空頭看漲期權足夠實值，你很可能會被分配到行權。如果你忘了要在發股利的前一天行權，而被強制分配行權，這可能使你遭受不小的損失，金額取決於股利的大小。另外，行權和分配都要繳納費用，除非你的交易量很大，否則對你來說是不小的成本。因為費用是按“每筆”計算的，而不是“每張合約”。也就是說，你行權一張＄55看漲期權合約與100張＄55看漲期權合約的價格是相同的。

因此，總的來說，借方價差組合應該是多頭邊為一單位實值期權，空頭邊為一單位虛值期權。

蝶式期權

雖然很多交易員說他們以交易蝶式期權謀生，我卻發現自己用蝶式期權賺錢的能力非常有限。我們來考察一下蝶式期權的內在特征，並探討為什么它比較難獲得高收益。

一個多頭的蝶式組合包含一個多頭價差和一個空頭價差，其中空頭邊與兩個多頭邊的執行價格之間的距離相等。例如，28/29/30看跌蝶式組合就是買一個28看跌期權，賣出兩個29看跌期權，買一個30看跌期權。我們的最大收益是當股票到期時落在兩個29的看跌執行價格上，這樣我們從30看跌期權中賺取＄1，而其他三個期權到期無價值。像這種一單位執行價格的蝶式組合，通常價格非常便宜，但究竟便宜多少要取決於兩個變量。第一個，我們先來看看波動率對該蝶式組合的影響。由於這筆交易僅在股票到期落在某個特定的執行價格上時才能獲得比較理想的收益，所以我們暫不用vega來衡量，而是看看波動率對股票概率分布曲線的影響來加以解釋。

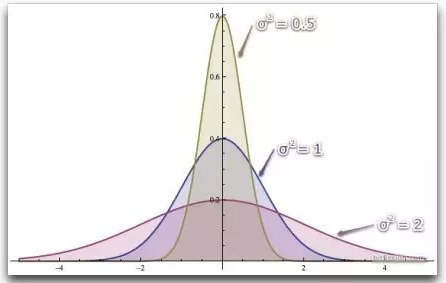
圖1：波動率對蝶式組合的影響

從圖中可以看到，隨著隱含波動率的上升，股票到期時落在某一個特定價格上的概率下降。因為這是在蝶式期權中唯一能夠賺錢的方式（股票到期時落在空頭執行價格上或附近），波動率越高，蝶式期權的交易價格越低，反之亦然。再看vega，由於這是一個較窄的價差組合（多頭價差為29/30看跌價差，空頭價差為28/29看跌價差），該蝶式組合中的vega很小。因此，盡管高波動率使蝶式期權變得便宜，但可能也就便宜一兩分錢。

蝶式期權具有一個特征，即使它能夠盈利，我們也說直到快要到期的那幾天，它才會“展開雙翅”。回到前面的圖中，我們可以把“較高波動率”替換為“距到期日更長”，“較低波動率”替換為“距到期日更短”。這樣替換之后，我們所討論的希臘值就變成了theta。theta，或時間衰減作用隨著到期日的臨近會以幾何級數增加。

如果我們把分布曲線的中點作為蝶式期權的空頭執行價格，隨著到期日的臨近，曲線變得狹窄而陡峭。我們的多頭執行價格落在曲線之外，外在價值逐漸接近為0，時間衰減作用相比之下沒那么高。但是我們的空頭執行價格的時間衰減作用是十分劇烈的。正是這種時間衰減的作用使得蝶式期權在其生命周期的末端“展開雙翅”，蝶式期權的價格迅速上升。但如果股票價格在任意方向上變動＄0.50，蝶式期權的衰減作用將迅速消退，“翅膀”也“展開”地更慢了些（或者甚至沒有“展開”）。隨著股價持續變動，“翅膀”可能又逐漸“閉合”了。以上的例子描述了蝶式期權變化無常的特征。

總結起來，購買蝶式期權是一種低成本、低概率的交易。若想獲取不錯的收益，即使市場如我所愿，也要持有到臨近到期時才能實現。

鐵鷹期權

鐵鷹期權組合由兩個貸方價差組成，一個看漲價差，一個看跌價差。一般來說，兩個價差都是虛值的，但並不做強制要求。必要的是，看跌期權價差所包含的執行價格要低於看漲期權價差的執行價格，並且二者的執行價格之間沒有重合。

回到前文中＄30股票的例子，一個空頭鐵鷹期權價差可能由空頭28/29看跌價差和空頭31/32看漲價差所組成。正如貸方價差的例子中所指出的，執行價格之間越接近，波動率對價差的影響就越小，因為相近的執行價格之間vega差別很微小。當然，這里由於使用了兩個貸方價差，所以vega大約是一個單獨的貸方價差的兩倍，而且鐵鷹交易是非方向性的，這與貸方價差不同。但是你可以將執行價格擴寬來增加價差組合的vega，使其獲得更多的波動率敞口。你也可以增加方向元素，不用對稱的執行價格來構建。

當較小的、保護性期權的價值很低（執行價格較寬）時，鐵鷹期權看起來就像一個寬跨式期權（將在非界定風險規則中討論）。這意味著，鐵鷹組合越寬，它對隱含波動率水平就越敏感，因此在波動率水平相對較高的環境中賣出時，將獲得更高的盈利概率和利潤率。鐵鷹組合如果很窄，即使在隱含波動率水平相對較高的環境中賣出會表現略佳，但也僅比一般波動率水平的環境中好一點點。

我想再次強調，如果沒有隱含波動率均值回歸的假設，空頭期權交易的優勢就要小得多。雖然隱含波動率約90%的時間都大於歷史波動率，僅僅這一點就為空頭期權交易創造了優勢。但是，有限的獲利能力加上無限的風險（如果是界定風險規則，雖然不是無限，但可能很大），這種特征可能會抹掉交易的大部分優勢，除非對交易管理得非常恰當。但是如果你的交易中隱含波動率的組成部分非常小或幾乎不存在，那么隱含波動率與歷史波動率之間的差別就是你唯一的優勢了。隨著你擴大鐵鷹組合的執行價格寬度，你也增加了風險。但如果能利用到隱含波動率均值回歸的額外優勢，我相信你的交易的預期收益率將大大提升，因為你優化了自己的風險回報情景。這樣做的風險更高，但如果管理得當的話，你會獲得豐厚的回報。

非界定風險交易

如前文所述，所有期權交易都是風險轉移的交易。如果你想讓我來承擔你的風險，那么你要支付我認為滿意的價格。這整部書就是在講風險轉移交易的定價，以及如何管理所接受到的風險。但我並沒有使用嚴格的數學方法，而是以一種更常識性的規則方法來介紹。市面上有上百本書解釋如何用black-scholes模型、二叉樹模型以及蒙特卡洛模擬來定價，並且這些模型還有上千種變體，但極少有書介紹如何利用這些模型來獲得對你有利的概率。

了解這一點，我們現在來看一些常見的非界定風險的交易。我們稱這些風險是“非界定”的，其實並不準確，比如一個裸空頭看跌期權，你能夠遭受的最大損失是可以確定的，因為股票只能跌到0。但通常這種情況會造成巨大的、甚至是災難性的損失。因此這些交易應該被稱為“高風險規則”。雖然這樣說更準確，但“非界定風險交易”是行業慣用術語，所以在此我也就沿用這一說法。要進行這一類交易，我們要找的就是做空權利金的交易。如果我們購買權利金，只要管理適當，我們僅會損失支付的權利金部分。所以，購買權利金的交易永遠是界定風險交易。

另外，根據期權模型，一筆多頭權利金交易賺錢的概率永遠小於50%。但因為我想要概率站在我這邊，所以我幾乎總是持有“空頭權利金投資組合”。而且作為一個裸期權的權利金賣方，我所承擔的是“非界定的”或者非常高的風險，所以我在這些交易中希望找到更多的優勢。承受的風險越大，在交易中想要的優勢就越大。當然，我會通過恰當的倉位管理和有效的投資組合管理來控制風險。但由於我從中獲取了更多的優勢，這些才是我真正維持生計的交易。我估計自己每年88%的交易盈利來自於做空權利金、非界定風險的交易。我前面也提到過，一旦你可以“將訓練輪子卸下來”，你就可以升級到這一類的交易中了。

跨式組合

跨式組合是買入（或賣出）一個看漲期權和一個看跌期權，執行價格相同，到期時間相同。如果你賣出了同樣數量的xyz股票的3月＄46看漲期權和3月＄46看跌期權，你就賣出了xyz的跨式組合。空頭的跨式組合持有雙邊風險。標的的任何大的變動都會造成損失，並且股票價格偏離跨式組合的損益平衡點越遠，所遭受的損失就越大。跨式組合通常以最接近股價的執行價格來交易（即平值執行價格），因此它是非方向性的。

由於平值期權具有最大的vega，而你賣出了兩個平值期權（每個跨式組合都包含一個看漲期權和一個看跌期權），因此這個規則的波動率部分是我們討論的所有規則中最大的。在實踐中，這意味著如果你根據我們前面所講的方式來選擇標的，該規則將提供最大的邊際優勢。利用隱含波動率的均值回歸性質，以及尋找正在放緩的歷史波動率來預測高隱含波動率股票將在交易的時間框架內均值回歸，我們希望“勝過”從跨式組合價格中所預測出的概率。如果我們能勝過預測概率，我們就能持續賺錢。

然而，跨式組合盡管可以給我們帶來最大盈利和最大交易優勢，它也持有最大風險。心臟不好的人不適合交易跨式組合。但是，另外有一種相近的規則，同樣提供較大盈利，並會提供一定的容錯緩沖。

寬跨式組合

空頭寬跨式期權，是做空一個虛值看跌期權和一個虛值看漲期權，到期時間相同。雖然實際上不一定兩個期權都要虛值，但我們通常是這樣來交易的。看漲期權必須要比看跌期權的執行價格高。

寬跨式組合可以不包含方向的偏好，兩邊賣出相同delta的期權，或盡可能相似。當然，由於存在典型的波動率偏度，這些期權與當前股價的距離未必對稱。但如果你相信期權定價是有效的，delta（或盈利概率）是衡量方向性風險的最佳指標，因此也是實現寬跨式期權無方向偏向性的最佳方法。當然，你也可以在交易中加入對方向的偏好，選擇不同delta的執行價格。這些選擇都基於你個人對於未來股票走勢的假設。

由於寬跨式組合的執行價格與當前標的價格的距離要比跨式組合更遠，因此寬跨式組合的vega比跨式組合要低。這意味著該交易與跨式組合相比，對於波動率的敏感度較低。但它仍然具有較強的vega部分，可能除了跨式之外，要高於所有其他規則。另外，與空頭跨式組合相比，寬跨式組合的損益平衡點與當前股價距離更遠，因此它比空頭跨式期權的盈利概率更高。雖然潛在收益值較低，但我幾乎總是選擇交易寬跨式組合，而不是跨式。而如果我選擇買入權利金交易，我會買跨式而不是寬跨式，因為這樣盈利概率更高。由於潛在收益的差別，我賣出的寬跨式組合要多於跨式組合。

總得來說，因為我是一個概率驅動的交易員，我利用隱含波動率的定價錯位來獲取優勢，空頭寬跨式組合是我最常用的交易規則。它的波動率部分足夠大，沒有方向的偏好，並且我可以調整損益平衡點，令其與當前股票價格的距離足夠遠，能夠使我高枕無憂。

【免責聲明】本文僅代表作者本人觀點，與本網站無關。本網站對文中陳述、觀點判斷保持中立，不對所包含內容的準確性、可靠性或完整性提供任何明示或暗示的保證。請讀者僅作參考，並請自行承擔全部責任。